Triangle of Power
Published 19/11/03, Edited 21/09/18
I was sitting in my Math 111 class the other day, doing some logarithms and minding my own business, when I saw a paper slowly start to slide into view. With it came the dreaded (and sometimes anticipated) question:
“Can you help me with this problem?”
The problem in question was \(5^{\log_5{6}+\log_5{7}}\). We simplified it to \(5^{\log_5{42}}\) easily enough, but the next step came harder. When I asked my young pupil what he thought it should be I saw a flash of panic cross is face.
This kid obviously didn’t do his homework I thought. So after a moment of pondering I decided to do what I normally do in these situations. I began to translate math into english.
“So if this is saying ‘5 to whatever power we raise 5 to to get 42’, what does that give us?”
“... 42?”
We had success! But while I had helped my friend learn his logs, I still left the class feeling dissatisfied. There has to be a better way to notate these I thought. So when I got home I went to see if the internet had come up with one.
And as the internet often has, it presented me with its gift, in this case The Triangle of Power.
This new notation was originally invented by alex.jordan in this answer to this Math Stack Exchange question. And it was later dubbed The Triangle of Power by 3Blue1Brown in this video.
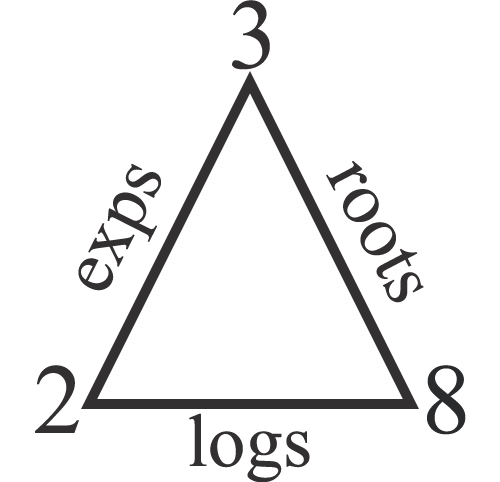
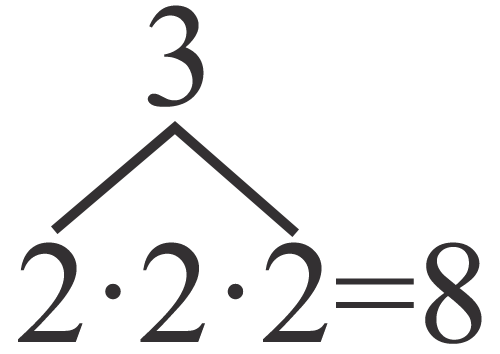
The triangle is essentially a method of notating the multiple multiplication relationship. Each side represents an operation: exponents, roots, or logs. And each corner represents a part of the relationship. The bottom left represents the “base factor”, the top is the exponent, and the bottom right is the product (since this is just multiplication I think calling things “factors” and “products” is fair).
There are two ways of using this notation. The first is where you fill in the full triangle. This makes it a static representation of a relationship.
\[\stackrel{y}{_x\triangle_{z}}\]
And the second way is to turn it into an equation.
\[\stackrel{y}{_x\triangle_{\phantom{z}}}=z\hspace{1em}|\hspace{1em}_x\triangle_{z}=y\hspace{.5em}...\]
The missing corner is then considered the result.
Identities
So having discovered this new notation, I had to try it on the problem from class.
\[5^{\log_5{42}}\longrightarrow\stackrel{_{\phantom{x}5}\triangle_{42}}{_5\triangle_{\phantom{z}}}\]
The second notation may not look much better at first, but if you remember what we said about the empty input representing the output, you can get a smooth mental picture of how this works.
\[\stackrel{_x\triangle_{z}}{_x\triangle_{\phantom{z}}}\longrightarrow\stackrel{\stackrel{y}{_x\triangle_{z}}}{_x\triangle_{\phantom{z}}}\longrightarrow\stackrel{\stackrel{y}{\downarrow}}{_x\triangle_{\phantom{z}}}\longrightarrow\stackrel{y}{_x\triangle_{\phantom{x}}}=z\]
The \(_x\triangle_{z}\) results in a value y. Then we raise x to the y. And we know from before that x to the y gives us z!
Writing it out using variables made me think of something else. The identity \(\stackrel{_x\triangle_{z}}{_x\triangle_{z}}\) actually works forwards and backwards!
\[\stackrel{_x\triangle_{z}}{_\phantom{x}\triangle_{z}}\longrightarrow\stackrel{\stackrel{y}{_x\triangle_{z}}}{_\phantom{x}\triangle_{z}}\longrightarrow\stackrel{\stackrel{y}{\downarrow}}{_\phantom{x}\triangle_{z}}\longrightarrow\stackrel{y}{_{\phantom{x}}\triangle_{z}}=x\]
If you are given two z’s instead of two x’s you know the output is x.
In the end you get a simple diagram the represents two different identities! And the lovely thing is that all six of the identities of two powers can be written this way, so that instead of six confusing expressions you get three lovely, memorable images.
\[\stackrel{_x\triangle_{z}}{_x\triangle_{z}}\hspace{3em}_x\stackrel{y}{\triangle}_{_x\stackrel{y}{\triangle}}\hspace{3em}_{{\stackrel{y}{\triangle}}_z}\stackrel{y}{\triangle}_z\] \[x^{\log_x{z}}=z\hspace{3em}\log_x{x^y}=y\hspace{3em}(\sqrt[y]{z})^y=z\] \[\sqrt[\log_x{z}]{z}=x\hspace{3em}\sqrt[y]{x^y}=x\hspace{3em}\log_{\sqrt[y]{z}}{z}=y\]
Functions and inverses
The next thing I knew I had to try the ToP (Triangle of Power) on was inverses. If you need a refresher, inverse functions map the outputs of a function to the inputs. It’s pretty easy to find an inverse function when you’re dealing with simple things like multiplication or addition, but it can be tricky with powers.
Luckily my teacher got around any conceptual confusion by telling us to trust her! /s
When she first introduced the class to logs she explained them as “logs are the inverse function of exponents”. This bugged me for a long time because I could have sworn I learned that roots were the inverse of exponents. But she showed that \(f(f’(x))=x\), so I was convinced I must have been misremembering.
I was not misremembering, we’ll get to that in a bit.
So how would we take a function like \(f(x)=2^x\) and find the inverse. Well we know that an inverse function takes the output of the original function and spits out the input.
And that logic actually maps nicely onto our new notation (as opposed to the old notation). We just take our output and make it our input.
Wonderful! And this logic works for things like x^2 as well:
\[_x{\stackrel{2}{\triangle}}\longrightarrow{_x{\stackrel{2}{\triangle}_y}}\longrightarrow\stackrel{2}{\triangle}_y\] \[f(x)={_x{\stackrel{2}{\triangle}}}\hspace{2em}f'(x)={\stackrel{2}{\triangle}_x}\]
Now if we write both of these in standard form we get the functions:
\[f(x)=2^x\hspace{1em}f'(x)=\log_2{x}\hspace{3em}f(x)=x^2\hspace{1em}f'(x)=\sqrt[2]{x}\]
This is what I don’t like about standard notation. It makes it too easy for a teacher to say “logs are the inverses of exponents” when it’s actually more complicated than that. It is better to think of these things as a relationship that describes a situation, in the way the ToP encourages.
If I want to find one piece of the relationship, I need to provide the other two.
Now seeing these inverse pairs written out makes me think of something else...
\[_2{\stackrel{x}{\triangle}}\hspace{1em}_2\triangle_x\hspace{3em}\stackrel{2}{\triangle}_x\hspace{1em}_x{\stackrel{2}{\triangle}}\hspace{3em}_x\triangle_2\hspace{1em}\stackrel{x}{\triangle}_2\]
All of these inverse pairs look an awful lot like our identities (if you imagine replacing the x of the left expression with the right expression).
\[\stackrel{_x\triangle_{z}}{_x\triangle_{z}}\hspace{3em}_x\stackrel{y}{\triangle}_{_x\stackrel{y}{\triangle}}\hspace{3em}_{{\stackrel{y}{\triangle}}_z}\stackrel{y}{\triangle}_z\]
Which is because in a way they are our identities! Both are about putting a function into an input. We just thought our way to them in a different way.
Advanced inverses
Now that I had figured out the basics of inverses, I wanted to see if I could do more advanced problems. Ones so scary I wouldn’t even want to touch them in standard notation!
This was a bit of a struggle at first, because I was focussing purely on symbol manipulation instead of understanding the concepts.
This lead me to do things like change \(_2{\stackrel{_3\triangle_x}{\triangle}}\) into \(_2{\triangle}_{_3{\stackrel{x}{\triangle}}}\), because I was just flipping the positions of all of the non-constants.
\[_2{\stackrel{_3\triangle_x}{\triangle}}\longrightarrow{_2{\stackrel{_3\stackrel{x}{\triangle}_\phantom{x}}{\triangle}}}\longrightarrow_2{\triangle}_{_3{\stackrel{x}{\triangle}}}\]
But the thing to remember about inverses is that you not only need to inverse the operations, you need to do them in reverse order otherwise you won’t be “undoing” the proper input.
The best method I’ve found for doing this was to work them forward to find the order and then reverse it.
\[_2{\stackrel{_3\triangle_x}{\triangle}}\longrightarrow{_2{\stackrel{y}{\triangle}}}\] \[_2{\stackrel{y}{\triangle}}\longrightarrow{_2\triangle_y}\longrightarrow_3{\triangle}_{_2\triangle_y}\longrightarrow{_3{\stackrel{_2\triangle_y}{\triangle}}}\]
But you can also work it by solving for x. Remember that the empty corner is our output, so we can switch that with what's on the other side of the equals.
\[_2{\stackrel{_3\triangle_x}{\triangle}}=y\] \[_2\triangle_y={_3\triangle_x}\] \[x={_3{\stackrel{_2\triangle_y}{\triangle}}}\]
Conclusion
In the beginning it may not have seemed like Triangle of Power notation would make much of a difference, but I think we’ve proven that it does! Identities are simple and readable. Inverses make so much more sense. And even solving complicated inverses is a breeze.
Try it out, and you’ll see just how much more fun it really is!