Lowest Common Ancestor
Published 10/10/20
The lowest common ancestor of of two vertices u and v in a directed acyclic graph is an ancestor of both u and v that has no descendant which is also an ancestor of both u and v.
Sounds pretty simple right? But if you actually try to come up with an efficient algorithm for finding the LCA of two nodes, it can be quite tricky.
Basic idea
The basic idea we’re going to use is that if we’re trying to find the LCA of two nodes u and v, and u is a descendant of v then the LCA is going to be v.
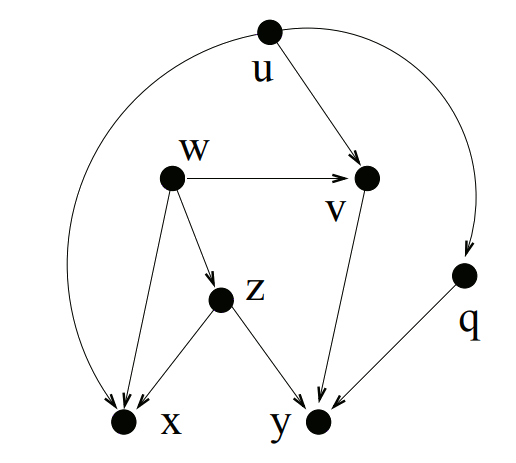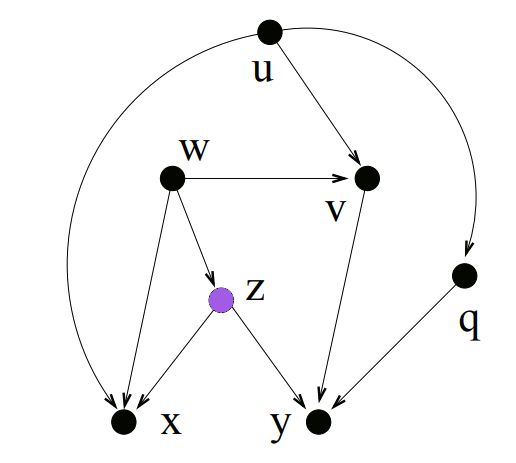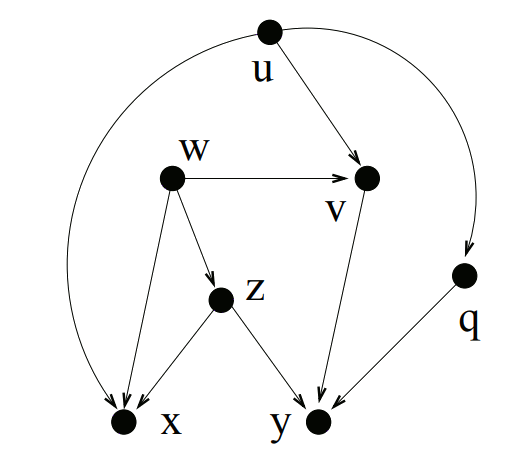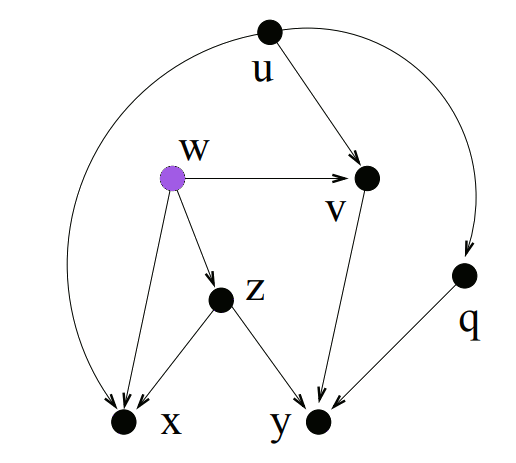
So if we first find all of the descendants of every node, we can use that info to find the LCA of every pair of nodes.
Also note that every node is a descendant of itself. This makes sense because if you try to find the LCA of a node and itself, the LCA is going to be the node.
Summary of implementation
The algorithm presented here has two preprocessing steps. After the preprocessing is completed you can find the LCA of any two nodes in your graph in constant time.
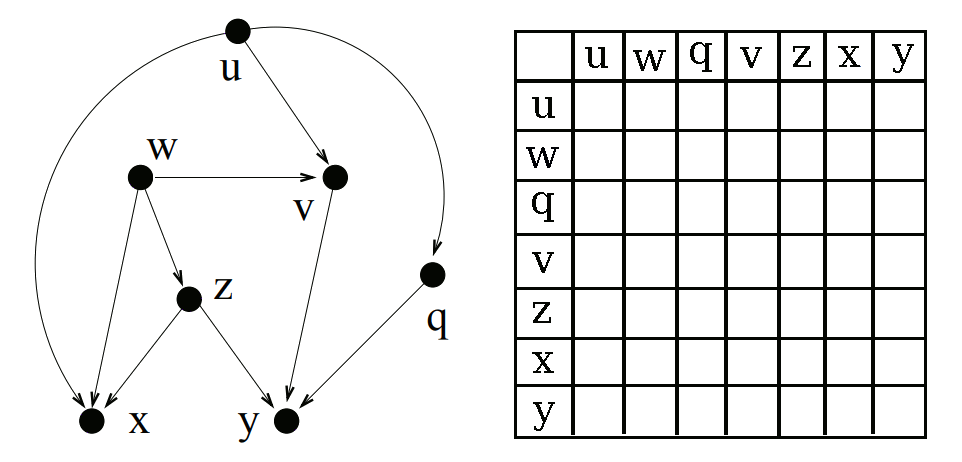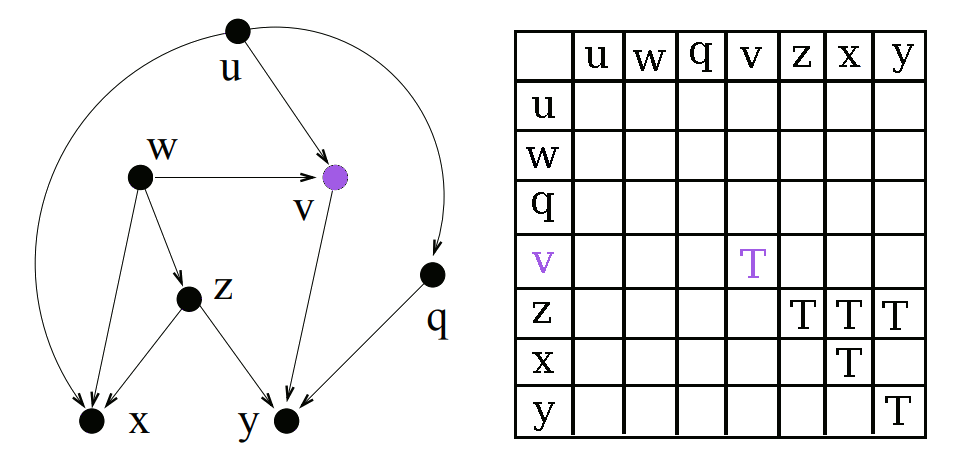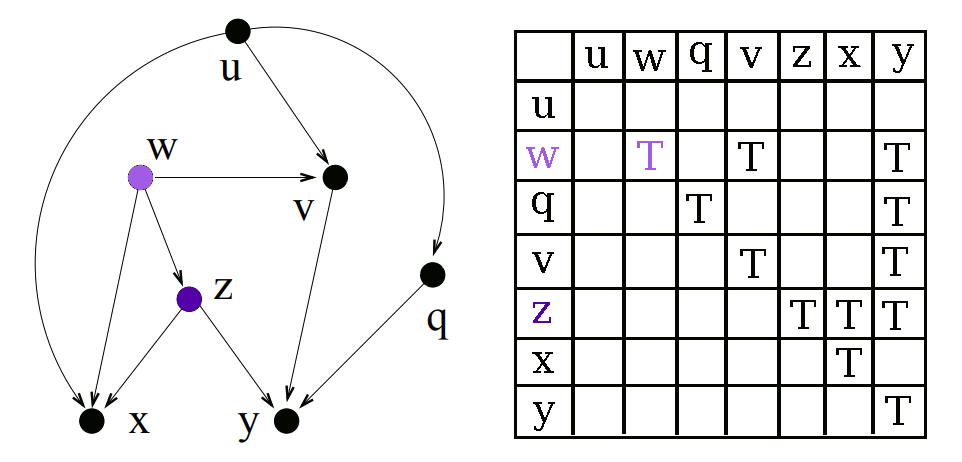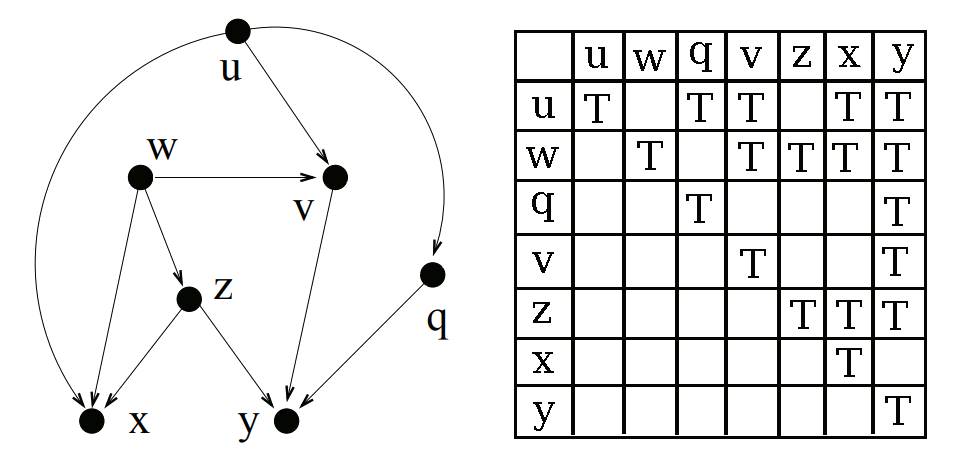
Step 1 creates a 2D boolean array which stores all of the descendants of every node. This is a temporary array that can be discarded when the algorithm is finished.
Step 2 creates a 3D node array which stores all of the LCAs of every pair of nodes. This array has to be kept around so that we can use it to do lookups.
These preprocessing steps have a time complexity of O(VE) where V is the number of vertices and E is the number of edges.
And while the finalized LCA array technically has a space complexity of O(V3), that would only be necessary if every node is connected to every other node. In most cases the space required will be closer to O(V2).
Step 1: Descendants table
Note: To simulate the 2D boolean array I’ll actually be using a 2D boolean map. This allows us to save space if we have a sparse graph.
function step1(graph) {
var descendantsMap = new Map();
var unvisitedNodes = new Set(graph.nodes);
while (!unvisitedNodes.isEmpty()) {
for (node of unvisitedNodes) {
// Check if it has an unvisited child.
var hasUnvisitedChildren = false;
for (child of node.children) {
if (unvisitedNodes.has(child)) {
hasUnvisitedChildren = true;
break;
}
}
if (hasUnvisitedChildren) {
continue;
}
// It is valid, so we can find the descendants.
var descendants = new Set(node);
for (child of node.children) {
for (descendant of descendantsMap.get(child)) {
descendants.add(descendant);
}
}
descendantsMap.set(node, descendants);
unvisitedNodes.remove(node);
}
}
}
First we find a node which has no unvisited direct children. For the initial pass this will be all of our leaf nodes. Once we have a node, we can start figuring out all of its descendants.
We know that every node is a descendant of itself, so we can add the node itself to the list of descendants immediately. Then for each of the node’s direct children, we add all of the child’s descendants to this node’s list of descendants.
Once a node has been “processed” (aka visited) we add it to the set of visited nodes. This allows us to visit the nodes in order from the leaves to the roots, filling up the descendants array.
Step 2: LCA table
The second stage of the algorithm is very similar to the first, except this time we work from the root nodes to the leaves.
function step2(graph, descendantsMap) {
var unvisitedNodes = new Set(graph.nodes);
while(!unvisitedNodes.isEmpty()) {
for (node of unvisitedNodes) {
// Check if it has an unvisited parent.
var hasUnvisitedParents = false;
for (child of node.parents) {
if (unvisitedNodes.has(parent)) {
hasUnvisitedParents = true;
break;
}
}
if (hasUnvisitedParents) {
continue;
}
// It is valid, so we can find the LCAs.
var LCAMap = new Map();
var descendants = descendantsMap.get(node);
for (otherNode of graph.nodes) {
var LCAs = new Set();
if (descendants.has(otherNode)) {
LCAs.add(node);
} else {
for (parent of node.parents) {
// lowestCommonAncestors is the global map.
var parentLCAs = lowestCommonAncestors
.get(parent).get(otherNode);
for (LCA of parentLCAs) {
LCAs.add(LCA);
}
}
for (LCA1 of LCAs) {
for (LCA2 of LCAs) {
if (LCA1 == LCA2) {
continue;
}
if (descendantsMap.get(LCA1).has(LCA2)) {
LCAs.remove(LCA1);
break;
}
}
}
}
LCAMap.set(otherNode, LCAs);
}
lowestCommonAncestors.set(node, LCAMap);
}
}
}
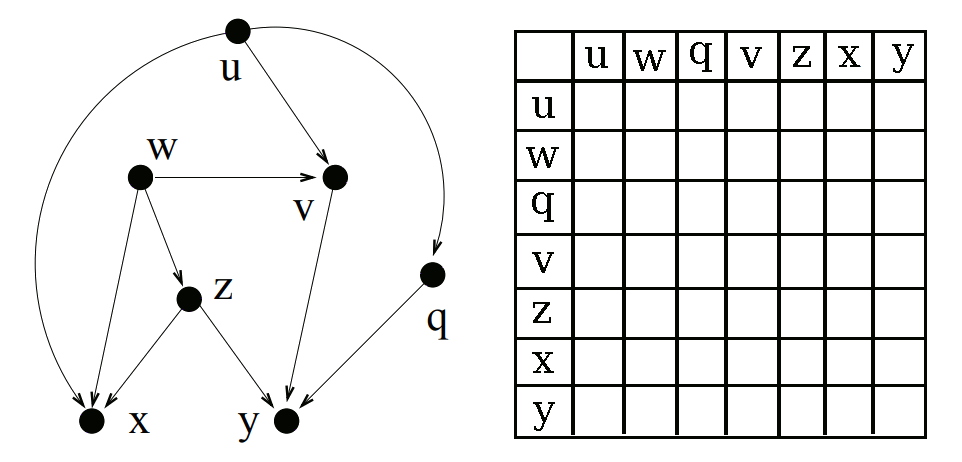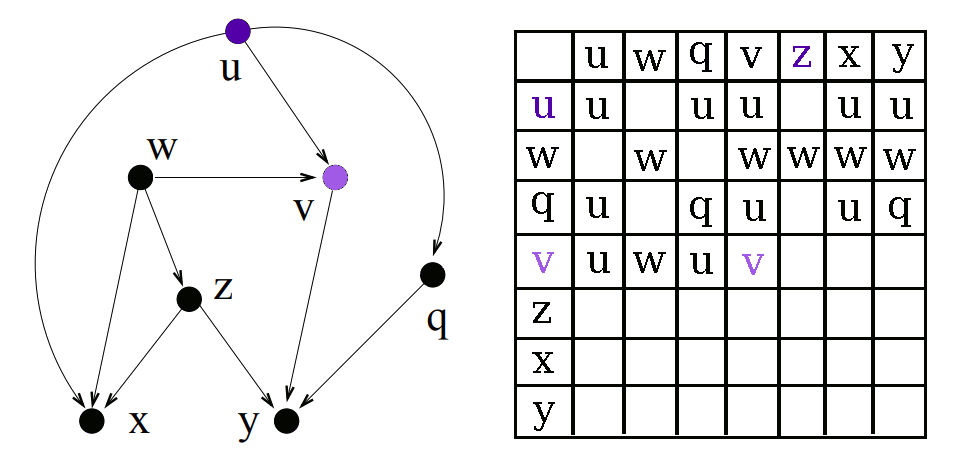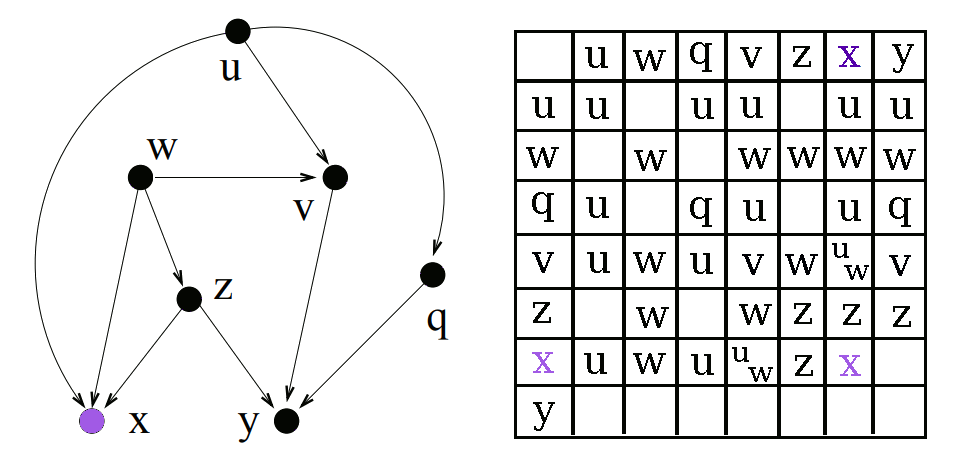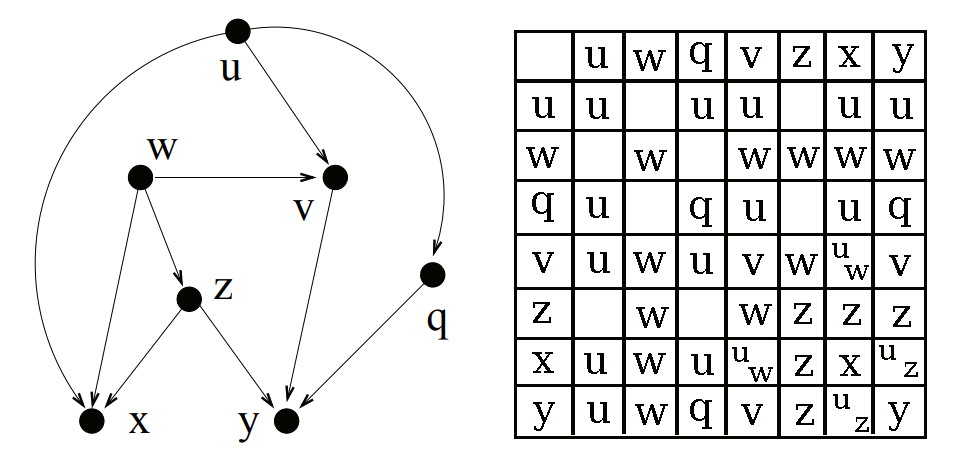
First we find a node which has no unvisited direct parents. For the initial pass this will be all of our root nodes. Once we have a node, we can start figuring out the lowest common ancestors it shares with each other node.
As discussed earlier, if we are trying to find the LCA of any node u and one of its descendants v, the LCA will be u. So we can look at the list of descendants for the node that we generated in Step 1 and immediately say that the current node is the LCA of itself and that node.
For all of the other nodes which are not descendants of the current node, we have to look at the direct parents of the current node. If a direct parent has a common ancestor with a node, we know that the current node also has a common ancestor with that node. So first we collect the set of all possible LCAs in all parents, and then we remove any LCA a which has a descendant which is also an LCA. That tells us a is not the lowest, and hence should not be included in the list.
Once a node has been “processed” (aka visited) we can add it to the list of visited nodes. This allows us to process nodes in order from roots to leaves, filling up the descendants array.
Lookups
function getLCAs(node1, node2) {
return lowestCommonAncestors.get(node1).get(node2);
}
Once we’ve created our array of LCAs we can easily lookup all of the LCAs of a given pair of nodes, and return it in constant time.
Bonus: LCA of multiple nodes
function getLCAs(...nodes) {
if (nodes.length < 2) {
return nodes;
}
return nodes.reduce((accumulator, currNode) => {
const LCAMap = lowestCommonAncestors.get(currNode);
return accumultator
.flatMap((node) => {
return LCAMap.get(node);
})
.filter(removeDuplicatesFn);
}, [nodes[0]]);
}
Finding the LCA of 3 or more nodes can also be easily done using stream processing. First we find the LCAs of the first two nodes. Then for each LCA we find the LCA of it and the third node. Then for each LCA generated by that we find the LCA of it and the fourth node… etc.
Conclusion
I hope you found this article helpful! If you want more info about how the time complexity of the preprocessing was determined, or any other info, there is a link to the original research paper below.
References
Czumaj, Artur, Miroslaw Kowaluk and Andrzej Lingas. "Faster algorithms for finding lowest common ancestors in directed acyclic graphs" Theoretical Computer Science, 380.1-2 (2007): 37-46.